If we talk about linear interpolation in Excel, we first need to understand what this term is. Linear interpolation is a method from mathematics that serves us to estimate values between two data points, if the data points are familiar.
In Excel, we can use linear interpolation with functions and formulas. In the example below, we will show how to do it.
Linear Interpolation in Excel
For our example, we will have two data points: (xy, y1) and (x2,y2). Our job will be to find the y-value corresponding to a certain x-value, that is located between x1 and x2.
To explain better, we will have the following table:
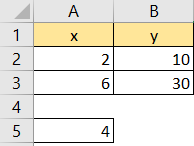
By looking at the table below, we could assume that following the logic of linear interpolation, the y2 number, located in cell A5 will be 20 since the progression of x is 2, and the progression of y is 10. To confirm this by formula, and generally to find the way to calculate it automatically, we will use the following formula in cell B5:
|
1 |
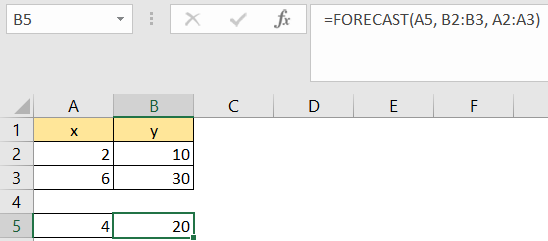
=FORECAST(A5, B2:B3, A2:A3) |
FORECAST formula has three parameters: x, known_ys, and known_xs
In our case, x is number 4, known_ys are 10 and 30, and known_xs are numbers 2 and 6.
This is the result we will end up with:
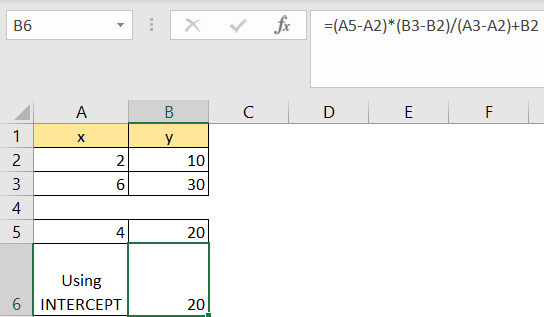
Instead of the FORECAST formula, we could also use INTERCEPT. Our formula in cell B6 will be:
|
1 |
=(A5-A2)*(B3-B2)/(A3-A2)+B2 |
To break down this formula:
- A5-A2 calculates the difference between the desired x-value and the lower known x-value.
- B3-B2 calculates the difference between the upper known y-value and the lower known y-value.
- A3-A2 calculates the difference between the upper known x-value and the lower known x-value.
This formula then multiplies the first two differences that we have and divides this result by the third difference in order to find the slope of the line connecting our two data points.
In the end, the formula adds the result to the lower known y-value to find the interpolated y-value for the given x-value.
We will get the same result using this formula, as we did with FORECAST:
Just remember- linear interpolation demands a straight-line relationship between the data points. If the data points are not linear, then we should use other interpolation methods.
